MoMaS: Mold Manifold Simulation for real-time procedural texturing
F. Maggioli, S. Melzi, M. Ovsjanikov, M. M. Bronstein, E. Rodolà
EUROGRAPHICS 2021 - Computer Graphics Forum
Abstract
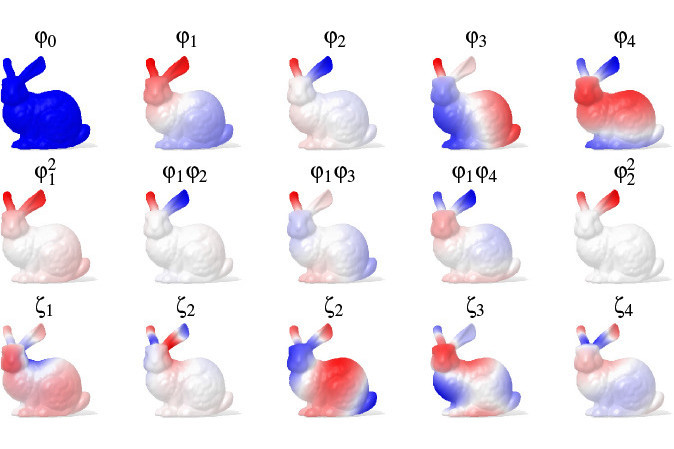
We propose a novel approach for the approximation and transfer of signals across 3D shapes. The proposed solution is based on taking pointwise polynomials of the Fourier-like Laplacian eigenbasis, which provides a compact and expressive representation for general signals defined on the surface. Key to our approach is the construction of a new orthonormal basis upon the set of these linearly dependent polynomials. We analyze the properties of this representation, and further provide a complete analysis of the involved parameters. Our technique results in accurate approximation and transfer of various families of signals between near-isometric and non-isometric shapes, even under poor initialization. Our experiments, showcased on a selection of downstream tasks such as filtering and detail transfer, show that our method is more robust to discretization artifacts, deformation and noise as compared to alternative approaches.
Rersources
BibTeX
@inproceedings{maggioli2021orthogonalized,
title={Orthogonalized fourier polynomials for signal approximation and transfer},
author={Maggioli, Filippo and Melzi, Simone and Ovsjanikov, Maksim and Bronstein, Michael M and Rodol{\`a}, Emanuele},
booktitle={Computer Graphics Forum},
volume={40},
number={2},
pages={435--447},
year={2021},
organization={Wiley Online Library}
}