Learning Spectral Unions of Partial Deformable 3D Shapes

L. Moschella, S. Melzi, L. Cosmo, F. Maggioli, O. Litany, M. Ovsjanikov, L. Guibas, E. Rodolà

EUROGRAPHICS 2022 - Computer Graphics Forum

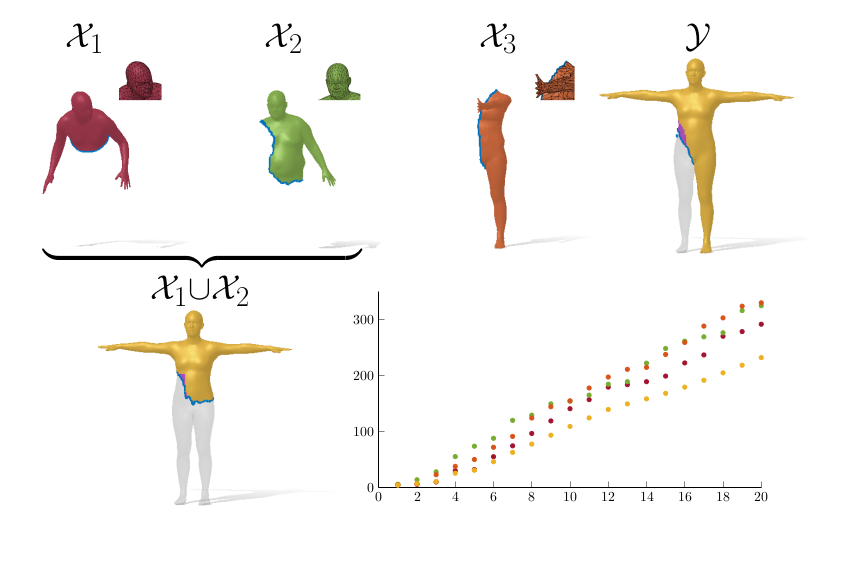
Spectral geometric methods have brought revolutionary changes to the field of geometry processing. Of particular interest is the study of the Laplacian spectrum as a compact, isometry and permutation-invariant representation of a shape. Some recent works show how the intrinsic geometry of a full shape can be recovered from its spectrum, but there are approaches that consider the more challenging problem of recovering the geometry from the spectral information of partial shapes. In this paper, we propose a possible way to fill this gap. We introduce a learning-based method to estimate the Laplacian spectrum of the union of partial non-rigid 3D shapes, without actually computing the 3D geometry of the union or any correspondence between those partial shapes. We do so by operating purely in the spectral domain and by defining the union operation between short sequences of eigenvalues. We show that the approximated union spectrum can be used as-is to reconstruct the complete geometry [MRC*19], perform region localization on a template [RTO*19] and retrieve shapes from a database, generalizing ShapeDNA [RWP06] to work with partialities. Working with eigenvalues allows us to deal with unknown correspondence, different sampling, and different discretizations (point clouds and meshes alike), making this operation especially robust and general. Our approach is data-driven and can generalize to isometric and non-isometric deformations of the surface, as long as these stay within the same semantic class (e.g., human bodies or horses), as well as to partiality artifacts not seen at training time.

PDF arXiv Code URL